* The next program I write will use what I have learned here to solve a high profile NP-Complete problem. With this type of accomplishment, I hope to bypass the multi-phase Google interview process, and conduct a single Pow-Wow interview session with Ken Thompson, Google's Most Distinguished Engineer.
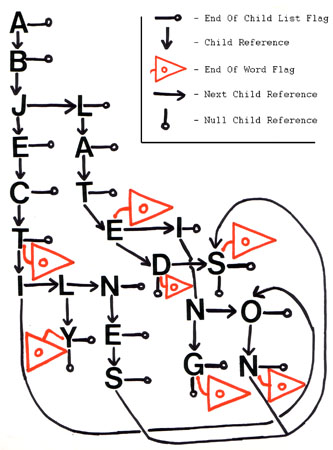
A directed acyclic word graph is simply a data structure that stores a lexicon of character strings or words in a compressed array of properly encoded integers. It is a great place to begin an investigation of lexicon-data-structure optimization, but ultimately, the traditional DAWG's limitations due to list-scrolling and Boolean return values will lead the elite-optimization-programmer to the more advanced Caroline Word Graph. Any process that makes use of the DAWG data structure traverses it as though it were a list-style trie. A TRIE is a data tree where every prefix is shared to reduce the amount of space required to store a lexicon and reduce the time required to “retrieve” a word. A Trie using explicit pointers, for each child node, becomes something like an enormous sparse matrix, populated mostly with zeros. Progression to a list-style Trie reduces the structure's size and retains the added benefit of a one-to-one ratio between words and End_Of_Word_Flags. The compromise is that finding a child node requires scrolling through a list of nodes. The DAWG data structure results from an attempt to reduce the size of a list-style Trie while maintaining the fast search times. This is carried out by attempting to replace identical postfix structures. It is critical to understand that all words ending with an “s” or “es” or “tion” or “istic” do NOT necessarily use the same nodes in the DAWG data structure. The example below will clarify this salient DAWG-property:
Consider the trie of 11 words stored in 23 nodes:|
|
 |
It can be clearly observed that because there is no “e” following the “t” in “abject,” the “t” contained in "ablate" can not be the same node in a DAWG. Hence the “tion” shared by each word does not share the same postfix structure, and must not be the same path in the DAWG. It is true however that the “ons” structure will be shared by both words in a DAWG. That is only true for the optimal DAWG because the “ons” part of “abjections” is a direct child. A graphical representation is presented above. It is not computer generated.
Due to the objective of space reduction being the essence of a DAWG, it is important to note that the minimal number of nodes will not produce the smallest DAWG. Space size of a data structure is given by the following equation:
STRUCTURE SIZE = (NUMBER OF NODES) x (SIZE OF EACH NODE)
The size of each node in computer science is not arbitrary. Data structures have a minimum unit size of 4-Bytes, and there are 1-Byte and 2-Byte basic integer types as well, but 3-Byte basic integer types do not exit. Standard C treats this as divine truth. Therefore if the size of each node can be reduced by half and the number of nodes does not double as a result, the total structure size has fallen. Replacing the Trie's Next pointer with breadth-first array population and a single Bit-Flag is why a DAWG-Node can fit into one 32-Bit integer. It is unfortunate that 3-Byte integers are not supported by modern processor architectures, because for TWL06, each int-node can be squeezed into 3-Bytes. There are 2 ways to make this happen even still, but they both require additional bit-manipulation instructions, so they can hardly be justified:
1) The DAWG structure can be housed in an array of short integers plus an array of chars. In this scheme, the first-child index value would span into both parts of the structure, and so additional masking and shifting would be required to extract information from each node. If the number of nodes in your DAWG can fit into 16 bits, then this 3-Byte segmentation is the way to go.A DAWG-Node can be seen as containing a letter, references to its children, and a Flag indicating the completion of a word. Now, because a single character does not represent an entire word, or key, computer science would not refer to (a single letter, a flag, and pointers) as a “node”. Rather, each character would be called an "edge". In order to simplify this DAWG treatment, the "edge" convention has been disposed of. A node in a DAWG is now defined as (an Explicit-Letter, an index to the First-Child node, an End-Of-Word flag, and an End-Of-List flag.
We are attempting to minimize the size of a single “node” so that it will be less than or equal to 32 bits while at the same time keeping the number of nodes low enough to justify the reduction of information in each node. For now, this is a double-edged sword, because it forces graph traversal to scroll through Child-Lists.
In short, the 26 letters in the English alphabet require 5-bits to store a Letter-Index, but since the space is available, we shall use a full 8-Bit Byte to store an Explicit-Letter, with the potential to accomodate languages with up to 256 unique characters. Additionally, no extra instruction will be needed to turn a Letter-Index into a usable char. Nodes need a single bit to store an End-Of-Word flag. A list of children should make sense because this would reduce the number of references for children to just two. One reference is for the First-Child of the list below a node, and a second reference is for Next-Node in the current list.
Experimentation has shown that there is one further reduction that will ultimately reduce the size of the final DAWG, but increase the number of nodes slightly. The DAWG nodes will be stored into a contiguous array, where the Next-Node reference will be replaced by a single End-Of-List bit-flag, where the Next-Node in a list is assumed to be the next element in the array unless the End-Of-List bit-flag is set. This will increase the total number of nodes required because the only DirectChild nodes will be tested for emilination, to keep the list structures intact, in other words, the first node in a Child-List is the only type of node where elimination can begin. Clearly, every node in the Next-List and every node below a redundant node will also be removed, so there will not be as much of a discrepancy in node elimination as one would expect, given this strict condition.
This "Child Reference Only" step is far from trivial, as it requires a “breadth” first tree traversal. This type of traversal is required to enter all of the temporary Tnodes into a 4D array which holds similar groups of pointers which will be sorted using 3 comparison values. Also, this type of traversal is required once more when assigning indexes to all of the remaining Tnodes. Complexity arises from the requirement of a secondary data structure know as a queue, so that traversal is carried out level by level, as opposed to the standard recursive “depth-first" traversal.
With ten bits spoken for, that leaves 22 bits remaining for the First-Child index. 22-Bits translates into a maximum number of array elements equal to 4,194,304. This value exceeds the number of nodes needed to store TWL06 by a large margin. TWL06 fits into 121,174 nodes (including the Null zero node), which requires only 17-bits. This number only reaches 123,670 nodes using a less complex algorithm, which used to be presented on this very page. Every node is a 4-Byte integer, so that is where 474 KB, presented above, comes from. At less than a half Mega Byte to store a fast Boolean graph of the English Language, the traditional DAWG encoding has its appeal. It would require almost double this space to store a DAWG with a minimal node count. Learn this data structure, and then migrate to the more advanced Caroline Word Graph.
The Blitzkrieg encoding places an Explicit-Letter into the first Byte of each Node-Integer, followed by the End-Of-List flag, followed by the End-Of-Word flag, and the final 22 most significant bits hold the First-Child index value, which can now be extracted using a single Bit-Shift. Below, I have included a printout of what each int-node looks like and the macros used to extract member data from them.
[1111111111111111111111|0|0|00000000] - CHILD_INDEX_BIT_MASK When creating a DAWG encoding with the Blitzkrieg_Trie_Attack algorithm, it will seem as though you have activated a time machine and transported the new DAWG data file into the PAST. Yes, the Blitzkrieg algorithm is that much faster than the older versions of Traditional_Dawg_Creator code, which took several minutes to compute TWL06 using even a 3Ghz multi-core PC. The 17 steps are listed below. Commented C-code is also provided, and will assist anyone who is interested in understanding how these steps actually work.
- The InternalValues integer contains all of the unique internal comparison values of each Tnode in one number.
- The CrcDigest value is calculated by using the InternalValues of each Tnode, and then building a longer data-message with information gathered from all Child nodes and Next nodes, seperated by pre-defined cypher integers. Tnodes without any Child or Next lists simply copy their InternalValues into their CrcDigest.
- The very heart of DAWG genesis, where the Blitzkrieg shines with CRC, and Tnode Grouping.
- Seperate groups exist for each [MaxChildDepth]-[LetterIndex] pair.
- Groups of similar Tnodes, are now sorted by 3 values, [BreadthFirst], [DirectChild], [CrcDigest].
- This Blitzkrieg Scheme means that each redundant Tnode patch will directly follow its living Tnode replacement.
Due to popular demand, there are Four versions of DAWG C-code published on this page. The oldest, more-basic code, the newest Blitzkrieg code, and two intermediate steps. Download the untampered with files below. The code being displayed is the dazzling Blitzkrieg Genesis code and a WildCard anagrammer. The C-code compiles just fine with "gcc -O3", so it works in Linux, and Windows using Cygwin. If you have an "Apple", I suggest that you decide to buy a real computer next time. For those who can tolerate Java, source code for the old web-start-app is also available:
Latest Blitzkrieg C-code:
// This program will compile a Traditional DAWG encoding from the "Word-List.txt" file. // Updated on Monday, December 29, 2011. // A graph compression algorithm this FAST is perfectly suited for record-keeping-compression while solving an NP-Complete. // 6 Major concerns addressed: // 0) A user defined character set of up to 256 letters is now supported. This accomodates certain foreign lexicons. // 1) Allowance for medium sized word lists. 2^22 DAWG node count is the new upper limit. // 2) Superior "ReplaceMeWith" scheme. // 3) The use of CRC-Digest calculation, "Tnode" segmentation, and stable group sorting render DAWG creation INSTANTANEOUS. // 4) Certain Graph configurataions led the previous version of this program to crash... NO MORE. // 5) A new DAWG int-node format is used to reduce the number of bitwise operations + add direct "char" extraction. // "Word-List.txt" is a text file with the number of words written on the very first line, and 1 word per line after that. // The words are case-insensitive for English letters, and the text file may have Windows or Linux format. // *** MAX is the length of the longest word in the list. Change this value. // *** MIN is the length of the shortest word in the list. Change this value. // Include the big-three header files. #include <stdlib.h> #include <stdio.h> #include <string.h> // General high-level program constants. #define MERGE_SORT_THRESHOLD 1 #define MIN 2 #define MAX 15 #define SIZE_OF_CHARACTER_SET 26 #define INPUT_LIMIT 35 #define LOWER_IT 32 #define TEN 10 #define INT_BITS 32 #define CHILD_BIT_SHIFT 10 // CHILD_INDEX_BIT_MASK is designed NEVER to be used. #define CHILD_INDEX_BIT_MASK 0XFFFFFC00 #define END_OF_WORD_BIT_MASK 0X00000200 #define END_OF_LIST_BIT_MASK 0X00000100 #define LETTER_BIT_MASK 0X000000FF #define CHILD_CYPHER 0X1EDC6F41 #define NEXT_CYPHER 0X741B8CD7 #define TWO_UP_EIGHT 256 #define LEFT_BYTE_SHIFT 24 #define BYTE_WIDTH 8 // C requires a boolean variable type so use C's typedef concept to create one. typedef enum { FALSE = 0, TRUE = 1 } Bool; typedef Bool* BoolPtr; // The lexicon text file. #define RAW_LEXICON "Word-List.txt" // This program will create "1" binary-data file for use, and "1" text-data file for inspection. #define TRADITIONAL_DAWG_DATA "Traditional_Dawg_For_Word-List.dat" #define TRADITIONAL_DAWG_TEXT_DATA "Traditional_Dawg_Explicit_Text_For_Word-List.txt" // An explicit table-lookup CRC calculation will be used to identify unique graph branch configurations. #define LOOKUP_TABLE_DATA "CRC-32.dat" unsigned int TheLookupTable[TWO_UP_EIGHT]; // Lookup tables used for node encoding and number-string decoding. const int PowersOfTwo[INT_BITS] = { 0X1, 0X2, 0X4, 0X8, 0X10, 0X20, 0X40, 0X80, 0X100, 0X200, 0X400, 0X800, 0X1000, 0X2000, 0X4000, 0X8000, 0X10000, 0X20000, 0X40000, 0X80000, 0X100000, 0X200000, 0X400000, 0X800000, 0X1000000, 0X2000000, 0X4000000, 0X8000000, 0X10000000, 0X20000000, 0X40000000, 0X80000000 }; const int PowersOfTen[TEN] = { 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000 }; const unsigned char CharacterSet[SIZE_OF_CHARACTER_SET] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z' }; // Some word lists will contain letters that NO words begin with. Place "0"s in the corresponding positions. const unsigned char EntryNodeIndex[SIZE_OF_CHARACTER_SET] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 }; // This simple function clips off the extra chars for each "fgets()" line. Works for Linux and Windows text format. void CutOffExtraChars(char *ThisLine){ if ( ThisLine[strlen(ThisLine) - 2] == '\r' ) ThisLine[strlen(ThisLine) - 2] = '\0'; else if ( ThisLine[strlen(ThisLine) - 1] == '\n' ) ThisLine[strlen(ThisLine) - 1] = '\0'; } // Returns "FALSE" if "TheWord" contains any character not defined in "CharacterSet", and "TRUE" otherwise. Bool TestForValidWord(const unsigned char *TheWord){ int Length = strlen(TheWord); int X; int Y; for ( X = 0; X < Length; X++ ) { for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { if ( TheWord[X] == CharacterSet[Y] ) goto NestedContinue; } return FALSE; NestedContinue:; } return TRUE; } // Return the index position of character "ThisChar", as it appears in "CharacterSet", and it must exist in the set. unsigned char CharToIndexConversion(unsigned char ThisChar){ int Y; for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { if ( ThisChar == CharacterSet[Y] ) return Y; } } // "TheWord" must consist of valid letters within "CharacterSet". // This function converts "TheWord" from actual characters into index values and stores them into "TheWordByIndex". void LettersToIndexConversion(const unsigned char *TheWord, unsigned char *TheWordByIndex){ int Length = strlen(TheWord); int X; for ( X = 0; X < Length; X++ ) { TheWordByIndex[X] = CharToIndexConversion(TheWord[X]); } } // Returns the positive "int" rerpresented by "TheNumberNotYet" string. An invalid "TheNumberNotYet" returns "0". int StringToPositiveInt(char* TheNumberNotYet){ int Result = 0; int X; int Length = strlen(TheNumberNotYet); if ( Length > TEN ) return 0; for ( X = 0; X < Length; X++ ) { if ( TheNumberNotYet[X] < '0' || TheNumberNotYet[X] > '9' ) return 0; Result += ((TheNumberNotYet[X] - '0')*PowersOfTen[Length - X - 1 ]); } return Result; } // The "BinaryNode" string must be at least 32 + 5 + 1 bytes in length. Space for the bits, // the seperation pipes, and the end of string char. // This function is used to fill the text file used to inspect the graph created in the first segment of the program. void ConvertIntNodeToBinaryString(int TheNode, char *BinaryNode){ int X; int Bit; BinaryNode[0] = '['; // 22 Bits, (31-->10) hold the First-Child index. Bit = 31; for ( X = 1; X <= 22; X++, Bit-- ) BinaryNode[X] = (TheNode & PowersOfTwo[Bit])?'1':'0'; BinaryNode[23] = '|'; // Bit 9 holds the End-Of-Word flag. BinaryNode[24] = (TheNode & END_OF_WORD_BIT_MASK)?'1':'0'; BinaryNode[25] = '|'; // Bit 8 holds the End-Of-List flag. BinaryNode[26] = (TheNode & END_OF_LIST_BIT_MASK)?'1':'0'; BinaryNode[27] = '|'; // The Letter is held in the final 8 bits, (7->0). Bit = 7; for ( X = 28; X <= 35; X++, Bit-- ) BinaryNode[X] = (TheNode & PowersOfTwo[Bit])?'1':'0'; BinaryNode[36] = ']'; BinaryNode[37] = '\0'; } //This Function converts any lower case letters inside "RawWord" to capitals, so that the whole string is made of capital letters. void MakeMeAllCapital(char *RawWord){ int Count = 0; int Length = strlen(RawWord); for ( Count = 0; Count < Length; Count++ ) { if ( RawWord[Count] >= 'a' && RawWord[Count] <= 'z' ) RawWord[Count] -= LOWER_IT; } } // This function performs a Byte-wise lookup table CRC calculation on "NumberOfBytes" Bytes, starting at "DataMessage". // The Polynomial used to generate the lookup table is CRC-32 = 0X04C11DB7. // The value returned by the function is the "CRC-Digest". unsigned int LookupTableCrc(const unsigned char *DataMessage, int NumberOfBytes, Bool Print){ int X; if ( Print ) { printf("|"); for ( X = 0; X < NumberOfBytes; X++ ) { printf("%02X", DataMessage[X]); if ( X%4 == 3 ) printf("|"); } printf(" - Length |%d|\n", NumberOfBytes); } // Because looking up "0" in the table returns "0", it is safe to use a table lookup to fill the "WorkingRegister" with its initial "DataMessage" value. register unsigned int WorkingRegister = 0; // Query the "LookupTable" exactly "NumberOfBytes" times. Perform lookups using the value inside of "WorkingRegister" as the index. // After each table query, "XOR" the value returned by "TheLookupTable" with "WorkingRegister" after pulling in the next Byte of "DataMessage". // "X" is the location of the next data Byte to pull into the calculation. for ( X = 0; X < NumberOfBytes; X++ ) WorkingRegister = TheLookupTable[WorkingRegister >> LEFT_BYTE_SHIFT] ^ ((WorkingRegister << BYTE_WIDTH) ^ DataMessage[X]); if ( Print ) printf("Calculated Digest = |%08X|\n", WorkingRegister); return WorkingRegister; } /*Trie to Dawg TypeDefs*/ struct tnode { struct tnode* Next; struct tnode* Child; struct tnode* ParentalUnit; struct tnode* ReplaceMeWith; // When populating the DAWG array, you must know the index assigned to each "Child". // "ArrayIndex" Is stored in every node, so that we can mine the information from the Trie. int ArrayIndex; int InternalValues; char DirectChild; unsigned char LetterIndex; char MaxChildDepth; char Level; unsigned char NumberOfChildren; unsigned char DistanceToEndOfList; char Dangling; char Protected; char EndOfWordFlag; unsigned int CrcDigest; // To streamline checking if "Protected" "Tnode"s are up for "Dangling", filter "ProtectedUnderCount" up to the root "Tnode"; do it on the fly. int ProtectedUnderCount; }; typedef struct tnode Tnode; typedef Tnode* TnodePtr; // Functions to access internal "Tnode" members. int TnodeArrayIndex(TnodePtr ThisTnode){ return ThisTnode->ArrayIndex; } char TnodeDirectChild(TnodePtr ThisTnode){ return ThisTnode->DirectChild; } TnodePtr TnodeNext(TnodePtr ThisTnode){ return ThisTnode->Next; } TnodePtr TnodeChild(TnodePtr ThisTnode){ return ThisTnode->Child; } TnodePtr TnodeParentalUnit(TnodePtr ThisTnode){ return ThisTnode->ParentalUnit; } TnodePtr TnodeReplaceMeWith(TnodePtr ThisTnode){ return ThisTnode->ReplaceMeWith; } unsigned char TnodeLetterIndex(TnodePtr ThisTnode){ return ThisTnode->LetterIndex; } char TnodeMaxChildDepth(TnodePtr ThisTnode){ return ThisTnode->MaxChildDepth; } unsigned char TnodeNumberOfChildren(TnodePtr ThisTnode){ return ThisTnode->NumberOfChildren; } unsigned char TnodeDistanceToEndOfList(TnodePtr ThisTnode){ return ThisTnode->DistanceToEndOfList; } char TnodeEndOfWordFlag(TnodePtr ThisTnode){ return ThisTnode->EndOfWordFlag; } char TnodeLevel(TnodePtr ThisTnode){ return ThisTnode->Level; } char TnodeDangling(TnodePtr ThisTnode){ return ThisTnode->Dangling; } char TnodeProtected(TnodePtr ThisTnode){ return ThisTnode->Protected; } unsigned int TnodeCrcDigest(TnodePtr ThisTnode){ return ThisTnode->CrcDigest; } // Allocate a "Tnode" and fill it with initial values. TnodePtr TnodeInit(unsigned char ChapIndex, TnodePtr OverOne, char WordEnding, char Leveler, int StarterDepth, TnodePtr Parent, char IsaChild, char StartListPosition){ TnodePtr Result = (Tnode *)malloc(sizeof(Tnode)); Result->LetterIndex = ChapIndex; Result->ArrayIndex = 0; Result->InternalValues = 0; Result->NumberOfChildren = 0; Result->DistanceToEndOfList = StartListPosition; Result->MaxChildDepth = StarterDepth; Result->Next = OverOne; Result->Child = NULL; Result->ParentalUnit = Parent; Result->Dangling = FALSE; Result->Protected = FALSE; Result->ReplaceMeWith = NULL; Result->EndOfWordFlag = WordEnding; Result->Level = Leveler; Result->DirectChild = IsaChild; Result->CrcDigest = 0; Result->ProtectedUnderCount = 0; return Result; } // Use this for debugging any program modifications. void TnodeOutput(TnodePtr ThisTnode){ printf("|%c|%d|%d|%d|%X|-|%X|\n", CharacterSet[ThisTnode->LetterIndex], ThisTnode->EndOfWordFlag, ThisTnode->NumberOfChildren, ThisTnode->DistanceToEndOfList, ThisTnode->InternalValues, ThisTnode->CrcDigest); if ( ThisTnode->Child != NULL ) TnodeOutput(ThisTnode->Child); } // Modify internal "Tnode" member values. void TnodeSetArrayIndex(TnodePtr ThisTnode, int TheWhat){ ThisTnode->ArrayIndex = TheWhat; } void TnodeSetChild(TnodePtr ThisTnode, TnodePtr Chump){ ThisTnode->Child = Chump; } void TnodeSetNext(TnodePtr ThisTnode, TnodePtr Nexis){ ThisTnode->Next = Nexis; } void TnodeSetParentalUnit(TnodePtr ThisTnode, TnodePtr Parent){ ThisTnode->ParentalUnit = Parent; } void TnodeSetReplaceMeWith(TnodePtr ThisTnode, TnodePtr Living){ ThisTnode->ReplaceMeWith = Living; } void TnodeSetMaxChildDepth(TnodePtr ThisTnode, int NewDepth){ ThisTnode->MaxChildDepth = NewDepth; } void TnodeSetDirectChild(TnodePtr ThisTnode, char Status){ ThisTnode->DirectChild = Status; } void TnodeFlyEndOfWordFlag(TnodePtr ThisTnode){ ThisTnode->EndOfWordFlag = TRUE; } // This statement evaluates to TRUE when the CRC at "one" has a higher value than the CRC at "two". "one" and "two" are indicies of "arrayone", and "arraytwo". #define COMPARE_TNODES(arrayone, one, arraytwo, two) ( arrayone[one]->CrcDigest > arraytwo[two]->CrcDigest ) void TnodeArrayMergeSortRecurse(TnodePtr *OriginalArray, int TheSize, TnodePtr *ExtraArray){ int FirstSize = TheSize>>1; int SecondSize = TheSize - FirstSize; int FirstIndex = 0; int SecondIndex = 0; int InsertIndex = 0; TnodePtr *TheFirst = OriginalArray; TnodePtr *TheSecond = OriginalArray + FirstSize; // Testing the escape condition before calling "TnodeArrayMergeSort" reduces stack overhead. if ( FirstSize > MERGE_SORT_THRESHOLD ) TnodeArrayMergeSortRecurse(TheFirst, FirstSize, ExtraArray); if ( SecondSize > MERGE_SORT_THRESHOLD ) TnodeArrayMergeSortRecurse(TheSecond, SecondSize, ExtraArray); // We can now conclude that the two lists are sorted, so merge them into the "ExtraArray". while ( FirstIndex < FirstSize && SecondIndex < SecondSize) { // Using this comparison macro ensures that the sort will be stable. if ( COMPARE_TNODES(TheSecond, SecondIndex, TheFirst, FirstIndex) ) { ExtraArray[InsertIndex] = TheSecond[SecondIndex]; SecondIndex += 1; InsertIndex += 1; } else { ExtraArray[InsertIndex] = TheFirst[FirstIndex]; FirstIndex += 1; InsertIndex += 1; } } // This instruction copies the remaining elements from the unfinished list into the "ExtraArray". if ( FirstIndex == FirstSize) memcpy(ExtraArray + InsertIndex, TheSecond + SecondIndex, (SecondSize - SecondIndex)*sizeof(TnodePtr)); else memcpy(ExtraArray + InsertIndex, TheFirst + FirstIndex, (FirstSize - FirstIndex)*sizeof(TnodePtr)); memcpy(OriginalArray, ExtraArray, TheSize*sizeof(TnodePtr)); } // After all words have been added to the initial Trie, this function will combine the internal comparison values of "ThisTnode" into its "InternalValues". void TnodeCalculateInternalValues(TnodePtr ThisTnode){ char *TheBytes = (char *)&(ThisTnode->InternalValues); TheBytes[0] = ThisTnode->LetterIndex; TheBytes[1] = ThisTnode->NumberOfChildren; TheBytes[2] = ThisTnode->DistanceToEndOfList; TheBytes[3] = ((ThisTnode->MaxChildDepth) << 1) + ThisTnode->EndOfWordFlag; } // Recursively calculate all "InternalValues" within a "Tnode" graph. "ThisTnode" must not be NULL. void TnodeCalculateInternalValuesRecurse(TnodePtr ThisTnode){ TnodeCalculateInternalValues(ThisTnode); if ( ThisTnode->Child != NULL ) TnodeCalculateInternalValuesRecurse(ThisTnode->Child); if ( ThisTnode->Next != NULL ) TnodeCalculateInternalValuesRecurse(ThisTnode->Next); } // The "CrcDigest" of a "Tnode" is heavily based on its "InternalValues". // Further, when a "Tnode" has a "Child" list OR it is NOT at the end of a list, // a data message is created using a series of "Child" and "NEXT" "CrcDigest"s. // These packets of data are seperated by "CYPHER" "int"s to distinguish "Tnode" branch structures. // Finally, a Byte-Wise Crc-Lookup-Table is used to convert the resulting data-message into a 32 bit "CrcDigest". void TnodeCalculateCrcDigest(TnodePtr ThisTnode, Bool Print){ static unsigned int TheMessage[(SIZE_OF_CHARACTER_SET + 2)<<1]; int MessageLength; int FillSpace; int X; TnodePtr Current; if ( ThisTnode->DistanceToEndOfList == 0 ) { // "ThisTnode" is a terminal node, so just use its "InternalValues" as its "CrcDigest". if ( ThisTnode->NumberOfChildren == 0 ) { ThisTnode->CrcDigest = (unsigned int)ThisTnode->InternalValues; return; } // "ThisTnode" has a "Child" list, but is located at the end of its own "Tnode" list. else { TheMessage[0] = (unsigned int)ThisTnode->InternalValues; TheMessage[1] = CHILD_CYPHER; MessageLength = ThisTnode->NumberOfChildren + 2; Current = ThisTnode->Child; for ( FillSpace = 2; FillSpace < MessageLength; FillSpace++ ) { TheMessage[FillSpace] = Current->CrcDigest; if ( TheMessage[FillSpace] == 0 ) printf("ZERO in CRC of Child.\n"); Current = Current->Next; } TheMessage[MessageLength] = (unsigned int)ThisTnode->InternalValues; MessageLength += 1; if ( Print == TRUE ) { for ( X = 0; X < MessageLength; X++ ) printf("|%08X", TheMessage[X]); printf("|\n"); } ThisTnode->CrcDigest = LookupTableCrc((unsigned char *)TheMessage, MessageLength<<2, Print); if ( Print == TRUE ) printf("Inherited Digest = |%X| - Length|%d|\n", ThisTnode->CrcDigest, MessageLength<<2); return; } } // "ThisTnode" has no "Child" list, but has following "Tnode"s in its own list. if ( ThisTnode->NumberOfChildren == 0 ) { TheMessage[0] = (unsigned int)ThisTnode->InternalValues; TheMessage[1] = NEXT_CYPHER; MessageLength = ThisTnode->DistanceToEndOfList + 2; Current = ThisTnode->Next; for ( FillSpace = 2; FillSpace < MessageLength; FillSpace++ ) { TheMessage[FillSpace] = Current->CrcDigest; if ( TheMessage[FillSpace] == 0 ) printf("ZERO in CRC of Next.\n"); Current = Current->Next; } TheMessage[MessageLength] = (unsigned int)ThisTnode->InternalValues; MessageLength += 1; ThisTnode->CrcDigest = LookupTableCrc((unsigned char *)TheMessage, MessageLength<<2, Print); return; } // "ThisTnode" has a "Child" list, and also has following "Tnode"s in its own list. TheMessage[0] = (unsigned int)ThisTnode->InternalValues; TheMessage[1] = CHILD_CYPHER; MessageLength = ThisTnode->NumberOfChildren + 2; Current = ThisTnode->Child; for ( FillSpace = 2; FillSpace < MessageLength; FillSpace++ ) { TheMessage[FillSpace] = Current->CrcDigest; if ( TheMessage[FillSpace] == 0 ) printf("ZERO in CRC of BChild.\n"); Current = Current->Next; } TheMessage[MessageLength] = NEXT_CYPHER; MessageLength += ThisTnode->DistanceToEndOfList + 1; Current = ThisTnode->Next; for ( FillSpace += 1; FillSpace < MessageLength; FillSpace++ ) { TheMessage[FillSpace] = Current->CrcDigest; if ( TheMessage[FillSpace] == 0 ) printf("ZERO in CRC of BNext.\n"); Current = Current->Next; } TheMessage[MessageLength] = (unsigned int)ThisTnode->InternalValues; MessageLength += 1; ThisTnode->CrcDigest = LookupTableCrc((unsigned char *)TheMessage, MessageLength<<2, Print); return; } // When calculating the "CrcDigest" of a "Tnode", its "Next" list and "Child" list must already have calculated "CrcDigest"s. void TnodeCalculateCrcDigestRecurse(TnodePtr ThisTnode){ if ( ThisTnode->Next != NULL ) TnodeCalculateCrcDigestRecurse(ThisTnode->Next); if ( ThisTnode->Child != NULL ) TnodeCalculateCrcDigestRecurse(ThisTnode->Child); TnodeCalculateCrcDigest(ThisTnode, FALSE); } // This function Dangles a "Tnode", but also recursively dangles every "Tnode" after and below it as well. // Dangling a "Tnode" means that it will be exculded from the final "DAWG" encoding. // By recursion, nodes that are not direct children will get dangled. // The function returns the total number of nodes dangled as a result. int TnodeDangleRecurse(TnodePtr ThisTnode){ int Result = 0; if ( ThisTnode->Dangling == TRUE ) return 0; if ( ThisTnode->Protected == TRUE ) { printf(" There is NO scenario where Dangling a Protected node should happen. ERROR, ERROR, ERROR.\n"); return 0; } if ( (ThisTnode->Next) != NULL ) Result += TnodeDangleRecurse(ThisTnode->Next); if ( (ThisTnode->Child) != NULL ) Result += TnodeDangleRecurse(ThisTnode->Child); if ( ThisTnode->Dangling == FALSE )Result += 1; ThisTnode->Dangling = TRUE; return Result; } // This function "Protects" a node being directly referenced in the elimination process. // "Protected" "Tnode"s should NEVER be "Dangling". // Make sure to increment "ProtectedUnderCount" by "1" all the way up to the root "Tnode". void TnodeProtect(TnodePtr ThisTnode){ TnodePtr Current = ThisTnode; if ( ThisTnode->Protected == FALSE ) { ThisTnode->Protected = TRUE; while ( Current != NULL ) { Current->ProtectedUnderCount += 1; Current = Current->ParentalUnit; } } } // This function returns the pointer to the "Tnode" in a parallel list of "Tnodes" with the "LetterIndex" "ThisLetterIndex", // and returns "NULL" if the "Tnode" does not exist. // If the function returns "NULL", then an insertion is required. TnodePtr TnodeFindParaNode(TnodePtr ThisTnode, unsigned char ThisLetterIndex){ TnodePtr Result = ThisTnode; if ( ThisTnode == NULL ) return NULL; if ( Result->LetterIndex == ThisLetterIndex ) return Result; while ( Result->LetterIndex < ThisLetterIndex ) { Result = Result->Next; if ( Result == NULL ) return NULL; } if ( Result->LetterIndex == ThisLetterIndex ) return Result; else return NULL; } // This function inserts a new "Tnode" before a larger "LetterIndex" "Tnode" or at the end of a para list. // If the list does not exist, then it is put at the beginnung. // The new "Tnode" has "ThisLetterIndex" in it. "AboveTnode" is the "Tnode" 1 level above where the new node will be placed. // This function should never be passed a "NULL" pointer. "ThisLetterIndex" should never exist in the "Child" "Tnode" list. void TnodeInsertParaNode(TnodePtr AboveTnode, unsigned char ThisLetterIndex, char WordEnder, int StartDepth){ AboveTnode->NumberOfChildren += 1; TnodePtr Holder = NULL; TnodePtr Currently = NULL; // Case 1: ParaList does not exist yet so start it. if ( AboveTnode->Child == NULL ) AboveTnode->Child = TnodeInit(ThisLetterIndex, NULL, WordEnder, AboveTnode->Level + 1, StartDepth, AboveTnode, TRUE, 0); // Case 2: "ThisLetterIndex" should be the first in the ParaList. else if ( AboveTnode->Child->LetterIndex > ThisLetterIndex ) { Holder = AboveTnode->Child; // The holder node is no longer a direct child so set it as such. TnodeSetDirectChild(Holder, FALSE); AboveTnode->Child = TnodeInit(ThisLetterIndex, Holder, WordEnder, AboveTnode->Level + 1, StartDepth, AboveTnode, TRUE, TnodeDistanceToEndOfList(Holder) + 1); // The parent node needs to be changed on what used to be the child. it is the Tnode in "Holder". Holder->ParentalUnit = AboveTnode->Child; } // Case 3: The ParaList exists and "ThisLetterIndex" is not first in the list. else { Currently = AboveTnode->Child; while ( Currently->Next !=NULL ) { if ( Currently->Next->LetterIndex > ThisLetterIndex ) break; Currently->DistanceToEndOfList += 1; Currently = Currently->Next; } Holder = Currently->Next; Currently->Next = TnodeInit(ThisLetterIndex, Holder, WordEnder, AboveTnode->Level + 1, StartDepth, Currently, FALSE, Currently->DistanceToEndOfList); Currently->DistanceToEndOfList += 1; if ( Holder != NULL ) Holder->ParentalUnit = Currently->Next; } } struct dawg { int NumberOfTotalWords; int NumberOfTotalNodes; TnodePtr First; }; typedef struct dawg Dawg; typedef Dawg* DawgPtr; // Set up the parent nodes in the Dawg. DawgPtr DawgInit(void){ DawgPtr Result = (Dawg *)malloc(sizeof(Dawg)); Result->NumberOfTotalWords = 0; Result->NumberOfTotalNodes = 0; Result->First = TnodeInit('0', NULL, FALSE, 0, 0, NULL, FALSE, 0); return Result; } // Return the root node of "ThisDawg", which is a direct child of the "First" node. TnodePtr DawgRootNode(DawgPtr ThisDawg){ return TnodeChild(ThisDawg->First); } // This function is responsible for adding "WordByIndexes" to the "Dawg" under its root node. // It returns the number of new nodes inserted. int TnodeDawgAddWord(TnodePtr ParentNode, const unsigned char *WordByIndexes, int WordSize){ int Result = 0; int X; int Y; TnodePtr HangPoint = NULL; TnodePtr Current = ParentNode; for ( X = 0; X < WordSize; X++){ HangPoint = TnodeFindParaNode(TnodeChild(Current), WordByIndexes[X]); if ( HangPoint == NULL ) { TnodeInsertParaNode(Current, WordByIndexes[X], (X == WordSize - 1 ? TRUE : FALSE), WordSize - X - 1); Result++; Current = TnodeFindParaNode(TnodeChild(Current), WordByIndexes[X]); for ( Y = X + 1; Y < WordSize; Y++ ) { TnodeInsertParaNode(Current, WordByIndexes[Y], (Y == WordSize - 1 ? TRUE : FALSE), WordSize - Y - 1); Result += 1; Current = TnodeChild(Current); } break; } else { if ( TnodeMaxChildDepth(HangPoint) < WordSize - X - 1 ) TnodeSetMaxChildDepth(HangPoint, WordSize - X - 1); } Current = HangPoint; // The path for the "WordByIndexes" that we are trying to insert already exists, // so just make sure that the end flag is flying on the last node. // This should never happen if we are to add words in alphabetical order and increasing "WordByIndexes" length. if ( X == WordSize - 1 ) TnodeFlyEndOfWordFlag(Current); } return Result; } // Add "NewWord" to "ThisDawg", which at this point is a "Trie" with a lot of information in each node. // "NewWord" must not exist in "ThisDawg" already. void DawgAddWord(DawgPtr ThisDawg, unsigned char *NewWordByIndexes, int WordLength){ ThisDawg->NumberOfTotalWords += 1; ThisDawg->NumberOfTotalNodes += TnodeDawgAddWord(ThisDawg->First, NewWordByIndexes, WordLength); } // This is a standard depth first inorder tree traversal. // Count un"Dangling" "Tnodes" into the 780 groups by "MaxChildDepth", "LetterIndex", and "DirectChild", then store values into "Tabulator". void TnodeGraphTabulateRecurse(TnodePtr ThisTnode, int ***Tabulator){ // We will only ever be concerned with "Living" nodes. "Dangling" Nodes will be eliminated, so don't count them. if ( ThisTnode->Dangling == FALSE ) { Tabulator[ThisTnode->MaxChildDepth][ThisTnode->LetterIndex][ThisTnode->DirectChild] += 1; // Go Down if possible. if ( ThisTnode->Child != NULL ) TnodeGraphTabulateRecurse(TnodeChild(ThisTnode), Tabulator); // Go Right if possible. if ( ThisTnode->Next != NULL ) TnodeGraphTabulateRecurse(TnodeNext(ThisTnode), Tabulator); } } // Count the "Living" "Tnode"s into the 780 groups by "MaxChildDepth", "LetterIndex", and "DirectChild", then store values into "Count". void DawgGraphTabulate(DawgPtr ThisDawg, int ***Count){ if ( ThisDawg->NumberOfTotalWords > 0 ) { TnodeGraphTabulateRecurse(TnodeChild(ThisDawg->First), Count); } } // Recursively replaces all redundant "Tnode"s under "ThisTnode", in one penetrating assult. // "DirectChild" "Tnode"s in a "Dangling" state have "ReplaceMeWith" set within them. void TnodeBlitzAttackRecurse(TnodePtr ThisTnode){ if ( ThisTnode->Next == NULL && ThisTnode->Child == NULL ) return; // The first "Tnode" being eliminated will always be a "DirectChild". if ( ThisTnode->Child != NULL ) { // The node is tagged to be excised, so replace it with "ReplaceMeWith". if ( ThisTnode->Child->Dangling == TRUE ) { ThisTnode->Child = ThisTnode->Child->ReplaceMeWith; } else { TnodeBlitzAttackRecurse(ThisTnode->Child); } } if ( ThisTnode->Next != NULL ){ TnodeBlitzAttackRecurse(ThisTnode->Next); } } // Replaces all pointers to "Dangling" "Child" "Tnodes" in the "ThisDawg" Trie with living ones. void BlitzkriegTrieAttack(DawgPtr ThisDawg){ TnodeBlitzAttackRecurse(ThisDawg->First->Child); } // A recursive function which Exchanges a single "Protected" "Tnode" under "ToDangle" with the corresponding "Tnode" under "ToKeep". // Remember to update "ProtectedUnderCount" for each line of "Tnodes" after the exchange. void TnodeExchangeProtectedNodeRecurse(TnodePtr ToDangle, TnodePtr ToKeep){ int ProtectedUnderCountParity; TnodePtr Holder; if ( ToDangle->Protected == TRUE) { if ( ToDangle->DirectChild == TRUE ) { //printf("Protected ToDangle = DirectChild"); if ( ToKeep->ReplaceMeWith == ToDangle ) { //printf(" - Standard Crosslink"); ProtectedUnderCountParity = ToDangle->ProtectedUnderCount - ToKeep->ProtectedUnderCount; Holder = ToDangle->ParentalUnit; while ( Holder != NULL ) { Holder->ProtectedUnderCount -= ProtectedUnderCountParity; Holder = Holder->ParentalUnit; } Holder = ToKeep->ParentalUnit; while ( Holder != NULL ) { Holder->ProtectedUnderCount += ProtectedUnderCountParity; Holder = Holder->ParentalUnit; } (ToKeep->ParentalUnit)->Child = ToDangle; (ToDangle->ParentalUnit)->Child = ToKeep; Holder = ToKeep->ParentalUnit; ToKeep->ParentalUnit = ToDangle->ParentalUnit; ToDangle->ParentalUnit = Holder; return; } // This case is not possible. else { return; } } // The "Protected" "Tnode" is not a "DirectChild". else { if ( ToKeep->Dangling == TRUE) { //printf(" - ToKeep = Dangling - Something is FUCKED up."); return; } else { //printf(" - ToKeep != Dangling"); ProtectedUnderCountParity = ToDangle->ProtectedUnderCount - ToKeep->ProtectedUnderCount; Holder = ToDangle->ParentalUnit; while ( Holder != NULL ) { Holder->ProtectedUnderCount -= ProtectedUnderCountParity; Holder = Holder->ParentalUnit; } Holder = ToKeep->ParentalUnit; while ( Holder != NULL ) { Holder->ProtectedUnderCount += ProtectedUnderCountParity; Holder = Holder->ParentalUnit; } (ToKeep->ParentalUnit)->Next = ToDangle; (ToDangle->ParentalUnit)->Next = ToKeep; Holder = ToKeep->ParentalUnit; ToKeep->ParentalUnit = ToDangle->ParentalUnit; ToDangle->ParentalUnit = Holder; return; } } } if ( ToDangle->Child != NULL ) TnodeExchangeProtectedNodeRecurse(ToDangle->Child, ToKeep->Child); if ( ToDangle->Next != NULL ) TnodeExchangeProtectedNodeRecurse(ToDangle->Next, ToKeep->Next); } //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// // A queue is required for breadth first traversal, and the rest is self-evident. struct breadthqueuenode { TnodePtr Element; struct breadthqueuenode *Next; }; typedef struct breadthqueuenode BreadthQueueNode; typedef BreadthQueueNode* BreadthQueueNodePtr; void BreadthQueueNodeSetNext(BreadthQueueNodePtr ThisBreadthQueueNode, BreadthQueueNodePtr Nexit){ ThisBreadthQueueNode->Next = Nexit; } BreadthQueueNodePtr BreadthQueueNodeNext(BreadthQueueNodePtr ThisBreadthQueueNode){ return ThisBreadthQueueNode->Next; } TnodePtr BreadthQueueNodeElement(BreadthQueueNodePtr ThisBreadthQueueNode){ return ThisBreadthQueueNode->Element; } BreadthQueueNodePtr BreadthQueueNodeInit(TnodePtr NewElement){ BreadthQueueNodePtr Result = (BreadthQueueNode *)malloc(sizeof(BreadthQueueNode)); Result->Element = NewElement; Result->Next = NULL; return Result; } struct breadthqueue { BreadthQueueNodePtr Front; BreadthQueueNodePtr Back; int Size; }; typedef struct breadthqueue BreadthQueue; typedef BreadthQueue* BreadthQueuePtr; BreadthQueuePtr BreadthQueueInit(void){ BreadthQueuePtr Result = (BreadthQueue *)malloc(sizeof(BreadthQueue)); Result->Front = NULL; Result->Back = NULL; Result->Size = 0; return Result; } void BreadthQueuePush(BreadthQueuePtr ThisBreadthQueue, TnodePtr NewElemental){ BreadthQueueNodePtr Noob = BreadthQueueNodeInit(NewElemental); if ( (ThisBreadthQueue->Back) != NULL ) BreadthQueueNodeSetNext(ThisBreadthQueue->Back, Noob); else ThisBreadthQueue->Front = Noob; ThisBreadthQueue->Back = Noob; (ThisBreadthQueue->Size) += 1; } TnodePtr BreadthQueuePop(BreadthQueuePtr ThisBreadthQueue){ if ( ThisBreadthQueue->Size == 0 ) return NULL; if ( ThisBreadthQueue->Size == 1 ) { ThisBreadthQueue->Back = NULL; ThisBreadthQueue->Size = 0; TnodePtr Result = (ThisBreadthQueue->Front)->Element; free(ThisBreadthQueue->Front); ThisBreadthQueue->Front = NULL; return Result; } TnodePtr Result = (ThisBreadthQueue->Front)->Element; BreadthQueueNodePtr Holder = ThisBreadthQueue->Front; ThisBreadthQueue->Front = (ThisBreadthQueue->Front)->Next; free(Holder); ThisBreadthQueue->Size -= 1; return Result; } // For the "Tnode" "Dangling" process, arrange the "Tnodes" in the "Holder" array, with breadth-first traversal order. void BreadthQueuePopulateReductionArray(BreadthQueuePtr ThisBreadthQueue, TnodePtr Root, TnodePtr ****Holder){ int InsertionPosition[MAX][SIZE_OF_CHARACTER_SET][2]; int CMCD; char CLetterIndex; char CDCstatus; memset(InsertionPosition, 0, 2*MAX*SIZE_OF_CHARACTER_SET*sizeof(int)); TnodePtr Current = Root; // Push the first row onto the queue. while ( Current != NULL ) { BreadthQueuePush(ThisBreadthQueue, Current); Current = Current->Next; } // Initiate the pop followed by push all children loop. while ( (ThisBreadthQueue->Size) != 0 ) { Current = BreadthQueuePop(ThisBreadthQueue); CMCD = Current->MaxChildDepth; CLetterIndex = Current->LetterIndex; CDCstatus = Current->DirectChild; Holder[CMCD][CLetterIndex][CDCstatus][InsertionPosition[CMCD][CLetterIndex][CDCstatus]] = Current; InsertionPosition[CMCD][CLetterIndex][CDCstatus] += 1; Current = TnodeChild(Current); while ( Current != NULL ) { BreadthQueuePush(ThisBreadthQueue, Current); Current = TnodeNext(Current); } } } // It is of absolutely critical importance that only "DirectChild" nodes are pushed onto the queue as child nodes. // This will not always be the case. // In a DAWG, a child pointer may point to an internal node in a longer list. Check for this. int BreadthQueueUseToIndex(BreadthQueuePtr ThisBreadthQueue, TnodePtr Root){ int IndexNow = 0; TnodePtr Current = Root; // Push the first row onto the queue. while ( Current != NULL ) { BreadthQueuePush(ThisBreadthQueue, Current); Current = Current->Next; } // Pop each element off of the queue and only push its children if its first "Child" is a "DirectChild", without a set "ArrayIndex". // Assign index if one has not been given to it yet. while ( (ThisBreadthQueue->Size) != 0 ) { Current = BreadthQueuePop(ThisBreadthQueue); // A traversal of the Trie will never land on "Dangling" "Tnodes", but it will try to visit certain "Tnodes" many times. // Even if we only "Push" "Tnode"s without an assigned "ArrayIndex", many "Tnode"s will have this value set while in the queue. if ( TnodeArrayIndex(Current) == 0 ) { IndexNow += 1; TnodeSetArrayIndex(Current, IndexNow); Current = TnodeChild(Current); if ( Current != NULL ) { // The graph will lead to intermediate positions, but we cannot start numbering "Tnodes" from the middle of a list. if ( TnodeDirectChild(Current) == TRUE && TnodeArrayIndex(Current) == 0 ) { while ( Current != NULL ) { if ( TnodeArrayIndex(Current) != 0 ) printf("Pushed Tnode with a non-zero ArrayIndex.\n"); BreadthQueuePush(ThisBreadthQueue, Current); Current = Current->Next; } } } } } return IndexNow; } //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// // Next and Child become indices. struct arraydnode{ int Next; int Child; unsigned char LetterIndex; char EndOfWordFlag; char Level; unsigned char ChildCount; unsigned char Position; }; typedef struct arraydnode ArrayDnode; typedef ArrayDnode* ArrayDnodePtr; void ArrayDnodeInit(ArrayDnodePtr ThisArrayDnode, unsigned char Chap, int Nextt, int Childd, char EndingFlag, char Breadth, unsigned char Posit, unsigned char Ccount){ ThisArrayDnode->LetterIndex = Chap; ThisArrayDnode->EndOfWordFlag = EndingFlag; ThisArrayDnode->Next = Nextt; ThisArrayDnode->Child = Childd; ThisArrayDnode->Level = Breadth; ThisArrayDnode->Position = Posit; ThisArrayDnode->ChildCount = Ccount; } void ArrayDnodeTnodeTranspose(ArrayDnodePtr ThisArrayDnode, TnodePtr ThisTnode){ ThisArrayDnode->LetterIndex = ThisTnode->LetterIndex; ThisArrayDnode->EndOfWordFlag = ThisTnode->EndOfWordFlag; ThisArrayDnode->Level = ThisTnode->Level; ThisArrayDnode->Position = ThisTnode->DistanceToEndOfList; ThisArrayDnode->ChildCount = ThisTnode->NumberOfChildren; if ( ThisTnode->Next == NULL ) ThisArrayDnode->Next = 0; else ThisArrayDnode->Next = (ThisTnode->Next)->ArrayIndex; if ( ThisTnode->Child == NULL ) ThisArrayDnode->Child = 0; else ThisArrayDnode->Child = (ThisTnode->Child)->ArrayIndex; } struct arraydawg { int NumberOfStrings; ArrayDnodePtr DawgArray; int First; }; typedef struct arraydawg ArrayDawg; typedef ArrayDawg* ArrayDawgPtr; //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// // This function is the core of the DAWG creation procedure. Pay close attention to the order of the steps involved. ArrayDawgPtr ArrayDawgInit(unsigned char **Dictionary, int *SegmentLenghts){ int X; int Y; int Z; int W; printf("Step 0 - Allocate the framework for the intermediate Array-Data-Structure.\n"); // Dynamically allocate the upper Data-Structure. ArrayDawgPtr Result = (ArrayDawgPtr)malloc(sizeof(ArrayDawg)); // Set NumberOfStrings. Result->NumberOfStrings = 0; for ( X = MIN; X <= MAX ; X++ ) Result->NumberOfStrings += SegmentLenghts[X]; printf("\nStep 1 - Create a TemporaryTrie and begin filling it with the |%d| words.\n", Result->NumberOfStrings); /// Create a Temp Trie structure and then feed in the given dictionary. DawgPtr TemporaryTrie = DawgInit(); for ( Y = MIN; Y <= MAX; Y++ ) { for ( X = 0; X < SegmentLenghts[Y]; X++ ) { DawgAddWord(TemporaryTrie, &(Dictionary[Y][Y*X]), Y); } } printf("\nStep 2 - Finished filling TemporaryTrie, so calculate the InternalValues comparison integers.\n"); TnodeCalculateInternalValuesRecurse(DawgRootNode(TemporaryTrie)); printf("\nStep 3 - Eliminate recursion by calculating the recursive CrcDigest for each Tnode.\n"); TnodeCalculateCrcDigestRecurse(DawgRootNode(TemporaryTrie)); printf("\nStep 4 - Count Tnodes into 780 groups, segmented by MaxChildDepth, Letter, and DirectChild.\n"); // Allocate 3D arrays of "int"s to count the "Tnodes" into groups. int ***NodeGroupCounter= (int ***)malloc(MAX*sizeof(int **)); int ***NodeGroupCounterInit = (int ***)malloc(MAX*sizeof(int **)); for ( X = 0; X < MAX; X++ ) { NodeGroupCounterInit[X] = (int **)malloc(SIZE_OF_CHARACTER_SET*sizeof(int *)); NodeGroupCounter[X] = (int **)malloc(SIZE_OF_CHARACTER_SET*sizeof(int *)); for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { NodeGroupCounterInit[X][Y] = (int *)calloc(2, sizeof(int)); NodeGroupCounter[X][Y] = (int *)calloc(2, sizeof(int)); } } DawgGraphTabulate(TemporaryTrie, NodeGroupCounterInit); printf("\nStep 5 - Initial Tnode counting is complete, so display results:\n"); int TotalNodeSum = 0; int MaxGroupSize = 0; int CurrentGroupSize; for ( X = 0; X < MAX; X++ ) { for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { CurrentGroupSize = NodeGroupCounterInit[X][Y][0] + NodeGroupCounterInit[X][Y][1]; TotalNodeSum += CurrentGroupSize; if ( CurrentGroupSize > MaxGroupSize ) MaxGroupSize = CurrentGroupSize; } } printf("\n Total Tnode Count For The Raw-Trie = |%d|, MaxGroupSize = |%d| \n", TotalNodeSum, MaxGroupSize); // We will have exactly enough space for all of the Tnode pointers. printf("\nStep 6 - Allocate a 4-D array of Tnode pointers to tag redundant Tnodes for replacement.\n"); TnodePtr ****HolderOfAllTnodePointers = (TnodePtr ****)malloc(MAX*sizeof(TnodePtr ***)); for ( X = 0; X < MAX; X++ ) { HolderOfAllTnodePointers[X] = (TnodePtr ***)malloc(SIZE_OF_CHARACTER_SET*sizeof(TnodePtr **)); for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { HolderOfAllTnodePointers[X][Y] = (TnodePtr **)malloc(3*sizeof(TnodePtr *)); CurrentGroupSize = NodeGroupCounterInit[X][Y][0] + NodeGroupCounterInit[X][Y][1]; if ( CurrentGroupSize ) { HolderOfAllTnodePointers[X][Y][2] = (TnodePtr *)malloc(CurrentGroupSize*sizeof(TnodePtr)); if ( NodeGroupCounterInit[X][Y][0] ) HolderOfAllTnodePointers[X][Y][0] = HolderOfAllTnodePointers[X][Y][2]; else HolderOfAllTnodePointers[X][Y][0] = NULL; if ( NodeGroupCounterInit[X][Y][1] ) { HolderOfAllTnodePointers[X][Y][1] = HolderOfAllTnodePointers[X][Y][2] + NodeGroupCounterInit[X][Y][0]; } else HolderOfAllTnodePointers[X][Y][1] = NULL; } else { HolderOfAllTnodePointers[X][Y][0] = NULL; HolderOfAllTnodePointers[X][Y][1] = NULL; HolderOfAllTnodePointers[X][Y][2] = NULL; } } } // A breadth-first traversal is used when populating the final array. // It is then much more likely for living "Tnode"s to appear first, if we fill "HolderOfAllTnodePointers" breadth first. printf("\nStep 7 - Populate the 4 dimensional Tnode pointer array, keeping DirectChild nodes closer to the end.\n"); // Use a breadth first traversal to populate the "HolderOfAllTnodePointers" array. BreadthQueuePtr Populator = BreadthQueueInit(); BreadthQueuePopulateReductionArray(Populator, DawgRootNode(TemporaryTrie), HolderOfAllTnodePointers); free(Populator); // "HolderOfAllTnodePointers" Population procedure is complete. printf("\nStep 8 - Use the stable Merge-Sort algorithm to sort [MaxChildDepth][LetterIndex] groups by CrcDigest values.\n"); TnodePtr *SupplementalArray = (TnodePtr *)malloc(MaxGroupSize*sizeof(TnodePtr)); for ( X = 0; X < MAX; X++ ) { for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { TnodeArrayMergeSortRecurse(HolderOfAllTnodePointers[X][Y][2], (NodeGroupCounterInit[X][Y][0] + NodeGroupCounterInit[X][Y][1]), SupplementalArray); } } free(SupplementalArray); // Flag all of the reduntant "Tnode"s, and store a "ReplaceMeWith" "Tnode" reference inside the "Dangling" "Tnode"s. // "Tnode"s are compared using their "CrcDigest" values, which incorporate information from entire branch structures. int NumberDangled; int DangledNow; int DirectDangled; int TotalDangled = 0; unsigned int CurrentCrcDigest; TnodePtr CorrectReplacementTnode; printf("\nStep 9 - Tag entire Tnode branch structures as Dangling - Elimination begins with DirectChild Tnodes and filters down:\n"); printf("\n This procedure is at the very heart of DAWG genesis, where the Blitzkrieg Algorithm shines with CRC, and Tnode Segmentation.\n"); printf(" Seperate groups exist for each [MaxChildDepth]-[LetterIndex] pair.\n"); printf(" Groups of similar Tnodes, are now sorted by 3 values, [BreadthFirst], [DirectChild], [CrcDigest].\n"); printf(" This Blitzkrieg Scheme means that each redundant Tnode patch will directly follow its living Tnode replacement.\n"); printf("\n ---------------------------------------------------------------------------------------------------------------------------\n"); // "X" is the current "MaxChildDepth". for ( X = MAX - 1; X >= 0; X-- ) { NumberDangled = 0; DirectDangled = 0; // "Y" is the current "LetterIndex", starting at "0". for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { CurrentGroupSize = NodeGroupCounterInit[X][Y][0] + NodeGroupCounterInit[X][Y][1]; CorrectReplacementTnode = NULL; CurrentCrcDigest = 0; // "Z" Will move through the current "Tnode" group, identifying the "CorrectReplacementTnode". for ( Z = 0; Z < CurrentGroupSize; Z++ ) { if ( HolderOfAllTnodePointers[X][Y][2][Z]->Dangling ) continue; CorrectReplacementTnode = HolderOfAllTnodePointers[X][Y][2][Z]; CurrentCrcDigest = CorrectReplacementTnode->CrcDigest; // "W" Tracks the "Tnodes" that will be Dangled, and shifts "Z" when it finds a new "CrcDigest". for ( W = Z + 1; W < CurrentGroupSize; W++ ) { if ( HolderOfAllTnodePointers[X][Y][2][W]->CrcDigest == CurrentCrcDigest) { if ( HolderOfAllTnodePointers[X][Y][2][W]->Dangling ) continue; if ( HolderOfAllTnodePointers[X][Y][2][W]->DirectChild == FALSE ) continue; // If the potential replacement "Tnode" has "Protected" "Tnode"s under it, then proceed to exchange the offending branch. if ( HolderOfAllTnodePointers[X][Y][2][W]->ProtectedUnderCount ) { printf(" Attempting to Dangle Protected, Count = |%d|", HolderOfAllTnodePointers[X][Y][2][W]->ProtectedUnderCount); TnodeExchangeProtectedNodeRecurse(HolderOfAllTnodePointers[X][Y][2][W], CorrectReplacementTnode); //printf(", after swap Count = |%d|.\n", HolderOfAllTnodePointers[X][Y][2][W]->ProtectedUnderCount); if ( HolderOfAllTnodePointers[X][Y][2][W]->ProtectedUnderCount ) { printf("\n Exchanging the first protected Tnode did not solve the problem. Fix the Exchange procedure.\n"); break; } else printf(" - FIXED.\n"); } HolderOfAllTnodePointers[X][Y][2][W]->ReplaceMeWith = CorrectReplacementTnode; TnodeProtect(CorrectReplacementTnode); DirectDangled += 1; DangledNow = TnodeDangleRecurse(HolderOfAllTnodePointers[X][Y][2][W]); NumberDangled += DangledNow; } else { Z = W - 1; break; } } } } printf(" DirectDangled |%5d| Tnodes, and |%5d| through recursion - MCD|%2d|\n", DirectDangled, NumberDangled, X); TotalDangled += NumberDangled; } printf(" ---------------------------------------------------------------------------------------------------------------------------\n\n"); int NumberOfLivingNodes; printf(" |%6d| = Original # of Tnodes.\n", TotalNodeSum); printf(" |%6d| = Dangled # of Tnodes.\n", TotalDangled); printf(" |%6d| = Remaining # of Tnodes.\n", NumberOfLivingNodes = TotalNodeSum - TotalDangled); printf("\nStep 10 - Count the number of living Tnodes by traversing the Raw-Trie to check the Dangling numbers.\n\n"); DawgGraphTabulate(TemporaryTrie, NodeGroupCounter); int TotalDangledCheck = 0; for ( X = 0; X < MAX; X++ ) { for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { for ( Z = 0; Z < 2; Z++ ) { TotalDangledCheck += (NodeGroupCounterInit[X][Y][Z] - NodeGroupCounter[X][Y][Z]); } } } if ( TotalDangled == TotalDangledCheck ) printf(" Tnode Dangling count is consistent, TotalDangledCheck = |%d|.\n", TotalDangledCheck); else printf(" MISMATCH for Tnode Dangling count.\n"); printf("\nstep 11 - Using the BlitzkriegTrieAttack, substitute Dangling Tnodes with internal \"ReplaceMeWith\" values.\n"); // Node replacement has to take place before indices are set up, so nothing points to redundant nodes. // This step is absolutely critical. Attack the Raw Trie using the Blitzkrieg single penetration. Then Index. BlitzkriegTrieAttack(TemporaryTrie); printf("\n Killing complete.\n"); printf("\nStep 12 - Blitzkrieg Attack is victorious, so assign array indicies to all living Tnodes using a Breadth-First-Queue.\n"); BreadthQueuePtr OrderMatters = BreadthQueueInit(); // The Breadth-First-Queue must assign an index value to each living "Tnode" only once. // Make sure to feed the root Tnode of "TemporaryTrie" into the "BreadthQueueUseToIndex()" function. int IndexCount = BreadthQueueUseToIndex(OrderMatters, DawgRootNode(TemporaryTrie)); free(OrderMatters); printf("\n Index assignment is now complete.\n"); printf("\n |%d| = NumberOfLivingNodes from after the Dangling process.\n", NumberOfLivingNodes); printf(" |%d| = IndexCount from the breadth-first assignment function.\n", IndexCount); // Allocate the space needed to store the "DawgArray". Result->DawgArray = (ArrayDnodePtr)calloc((NumberOfLivingNodes + 1), sizeof(ArrayDnode)); int IndexFollow = 0; int IndexFollower = 0; int TransposeCount = 0; // Roll through the pointer arrays and use the "ArrayDnodeTnodeTranspose" function to populate it. // Set the dummy entry at the beginning of the array. ArrayDnodeInit(&(Result->DawgArray[0]), 0, 0, 0, 0, 0, 0, 0); Result->First = 1; printf("\nStep 13 - Populate the new Working-Array-Dawg structure, used to verify validity and create the final integer-graph-encodings.\n"); // Scroll through "HolderOfAllTnodePointers" and look for un"Dangling" "Tnodes", if so then transpose them into "Result->DawgArray". for ( X = MAX - 1; X >= 0; X-- ) { for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { for (Z = 0; Z < 2; Z++ ) { for ( W = 0; W < NodeGroupCounterInit[X][Y][Z]; W++ ) { if ( TnodeDangling(HolderOfAllTnodePointers[X][Y][Z][W]) == FALSE ) { IndexFollow = TnodeArrayIndex(HolderOfAllTnodePointers[X][Y][Z][W]); ArrayDnodeTnodeTranspose(&(Result->DawgArray[IndexFollow]), HolderOfAllTnodePointers[X][Y][Z][W]); TransposeCount += 1; if ( IndexFollow > IndexFollower ) IndexFollower = IndexFollow; } } } } } printf("\n |%d| = IndexFollower, which is the largest index assigned in the Working-Array-Dawg.\n", IndexFollower); printf(" |%d| = TransposeCount, holds the number of Tnodes transposed into the Working-Array-Dawg.\n", TransposeCount); printf(" |%d| = NumberOfLivingNodes. Make sure that these three values are equal, because they must be.\n", NumberOfLivingNodes); if ( (IndexFollower == TransposeCount) && (IndexFollower == NumberOfLivingNodes) ) printf("\n Equality assertion passed.\n"); else printf("\n Equality assertion failed.\n"); // Conduct dynamic-memory-cleanup and free the whole Raw-Trie, which is no longer needed. for ( X = MAX - 1; X >= 0; X-- ) { for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { for ( W = 0; W < (NodeGroupCounterInit[X][Y][0] + NodeGroupCounterInit[X][Y][1]); W++ ) { free(HolderOfAllTnodePointers[X][Y][2][W]); } free(HolderOfAllTnodePointers[X][Y][2]); free(HolderOfAllTnodePointers[X][Y]); } free(HolderOfAllTnodePointers[X]); } free(HolderOfAllTnodePointers); free(TemporaryTrie); printf("\nStep 14 - Creation of the traditional-DAWG is complete, so store it in a binary file for use.\n"); FILE *Data; Data = fopen( TRADITIONAL_DAWG_DATA,"wb" ); // The "NULL" node in position "0" must be counted now. int CurrentNodeInteger = NumberOfLivingNodes + 1; // It is critical, especially in a binary file, that the first integer written to the file be the number of nodes stored in the file. fwrite( &CurrentNodeInteger, sizeof(int), 1, Data ); // Write the "NULL" node to the file first. CurrentNodeInteger = 0; fwrite( &CurrentNodeInteger, sizeof(int), 1, Data ); for ( X = 1; X <= NumberOfLivingNodes ; X++ ){ CurrentNodeInteger = (Result->DawgArray)[X].Child; CurrentNodeInteger <<= CHILD_BIT_SHIFT; CurrentNodeInteger |= CharacterSet[Result->DawgArray[X].LetterIndex]; if ( Result->DawgArray[X].EndOfWordFlag ) CurrentNodeInteger |= END_OF_WORD_BIT_MASK; if ( !Result->DawgArray[X].Next ) CurrentNodeInteger |= END_OF_LIST_BIT_MASK; fwrite(&CurrentNodeInteger, sizeof(int), 1, Data); } fclose(Data); printf( "\n The Traditional-DAWG-Encoding data file is now written.\n" ); printf("\nStep 15 - Output a text file with all the node information explicitly layed out.\n"); FILE *Text; Text = fopen(TRADITIONAL_DAWG_TEXT_DATA,"w"); char TheNodeInBinary[32+5+1]; int CompleteThirtyTwoBitNode; fprintf(Text, "Behold, the |%d| Traditional DAWG nodes are decoded below:\r\n\r\n", NumberOfLivingNodes); // We are now ready to output to the text file, and the "Main" binary data file. for ( X = 1; X <= NumberOfLivingNodes ; X++ ){ CompleteThirtyTwoBitNode = (Result->DawgArray)[X].Child; CompleteThirtyTwoBitNode <<= CHILD_BIT_SHIFT; CompleteThirtyTwoBitNode |= CharacterSet[Result->DawgArray[X].LetterIndex]; if ( (Result->DawgArray)[X].EndOfWordFlag == TRUE ) CompleteThirtyTwoBitNode |= END_OF_WORD_BIT_MASK; if ( (Result->DawgArray)[X].Next == 0 ) CompleteThirtyTwoBitNode |= END_OF_LIST_BIT_MASK; ConvertIntNodeToBinaryString(CompleteThirtyTwoBitNode, TheNodeInBinary); fprintf(Text, "N%6d-%s, DistanceToEndOfList|%2d|", X, TheNodeInBinary, Result->DawgArray[X].Position); fprintf(Text, ", NumberOfChildren|%2d|", Result->DawgArray[X].ChildCount); fprintf(Text, ", Lev|%2d|", (Result->DawgArray)[X].Level); fprintf(Text, ", {'%c',%d,%6d", CharacterSet[Result->DawgArray[X].LetterIndex], Result->DawgArray[X].EndOfWordFlag, Result->DawgArray[X].Next); fprintf(Text, ",%6d}", (Result->DawgArray)[X].Child); fprintf(Text, ".\r\n"); if ( CompleteThirtyTwoBitNode == 0 ) printf("\n Error in node encoding process.\n"); } fprintf(Text, "\r\nNumber Of Living Nodes |%d| Plus The NULL Node.\r\n\r\n", NumberOfLivingNodes); fclose(Text); return Result; } //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// int main(){ int X; int Y; unsigned char ThisLine[INPUT_LIMIT] = "\0"; printf("\n Hit \"Enter\" to begin the Blitzkrieg Attack Algorithm:\n\n Be dazzled, your DAWG will be created in the PAST:"); fgets(ThisLine, INPUT_LIMIT, stdin); // All of the words of similar length will be stored sequentially in the same array so that there will be (MAX + 1) arrays in total. // The Smallest length of a string is assumed to be 2. unsigned char *AllWordsInEnglish[MAX + 1]; for ( X = 0; X < (MAX + 1); X++ ) AllWordsInEnglish[X] = NULL; // Read the precompiled lookup-table from "CRC-32.dat" directly into "TheLookupTable". FILE *TableFile; TableFile = fopen(LOOKUP_TABLE_DATA, "rb"); fread(TheLookupTable, sizeof(unsigned int), TWO_UP_EIGHT, TableFile); fclose(TableFile); FILE *Input; Input = fopen(RAW_LEXICON,"r"); int FirstLineIsSize; int LineLength; fgets(ThisLine, INPUT_LIMIT, Input); CutOffExtraChars(ThisLine); FirstLineIsSize = StringToPositiveInt(ThisLine); printf("\n FirstLineIsSize = Number-Of-Words = |%d|\n", FirstLineIsSize); int DictionarySizeIndex[MAX + 1]; for ( X = 0; X <= MAX; X++ ) DictionarySizeIndex[X] = 0; char **LexiconInRam = (char**)malloc(FirstLineIsSize*sizeof(char *)); // The first line is the Number-Of-Words, so read them all into RAM, temporarily. for ( X = 0; X < FirstLineIsSize; X++ ) { fgets(ThisLine, INPUT_LIMIT, Input); CutOffExtraChars(ThisLine); MakeMeAllCapital(ThisLine); if ( !TestForValidWord(ThisLine) ) printf("Invalid Word @ |%d|-|%s|\n", X, ThisLine); LineLength = strlen(ThisLine); if ( LineLength <= MAX ) DictionarySizeIndex[LineLength] += 1; else { printf("The word in position |%d| is too long. EXIT.\n", X); return 0; } LexiconInRam[X] = (unsigned char *)malloc((LineLength + 1)*sizeof(unsigned char)); strcpy(LexiconInRam[X], ThisLine); } printf("\n Word-List.txt is now in RAM.\n"); // Allocate enough space to hold all of the words in "unsigned char" arrays holding character indexes. for ( X = 2; X < (MAX + 1); X++ ) AllWordsInEnglish[X] = (unsigned char *)malloc(X*DictionarySizeIndex[X]*sizeof(unsigned char)); int CurrentTracker[MAX + 1]; memset(CurrentTracker, 0, (MAX + 1)*sizeof(int)); unsigned char CurrentWordByIndex[MAX]; int CurrentLength; // Copy all of the words into the "LetterIndex" format "AllWordsInEnglish" array. for ( X = 0; X < FirstLineIsSize; X++ ) { CurrentLength = strlen(LexiconInRam[X]); // Convert each string from its temporary ram location into the "LetterIndex" format, and copy that into "AllWordsInEnglish". LettersToIndexConversion(LexiconInRam[X], CurrentWordByIndex); memcpy(AllWordsInEnglish[CurrentLength] + CurrentTracker[CurrentLength]*CurrentLength, CurrentWordByIndex, CurrentLength); CurrentTracker[CurrentLength] += 1; } printf("\n The words are now stored in an array according to length.\n\n"); // Make sure that the counting has resulted in all of the strings being placed correctly. for ( X = 0; X < (MAX + 1); X++ ) { if ( DictionarySizeIndex[X] == CurrentTracker[X] ) printf(" |%2d| Letter word count = |%5d| is verified.\n", X, CurrentTracker[X]); else printf(" Something went wrong with |%2d| letter words.\n", X); } // Free the the initial dynamically allocated memory. for ( X = 0; X < FirstLineIsSize; X++ ) free(LexiconInRam[X]); free(LexiconInRam); printf("\n Begin Creator init function.\n\n"); ArrayDawgPtr Adoggy = ArrayDawgInit(AllWordsInEnglish, DictionarySizeIndex); printf("\nStep 16 - Display the Mask-Format for the DAWG int-nodes:\n\n"); char Something[32+5+1]; ConvertIntNodeToBinaryString(CHILD_INDEX_BIT_MASK, Something); printf(" %s - CHILD_INDEX_BIT_MASK\n", Something); ConvertIntNodeToBinaryString(END_OF_WORD_BIT_MASK, Something); printf(" %s - END_OF_WORD_BIT_MASK\n", Something); ConvertIntNodeToBinaryString(END_OF_LIST_BIT_MASK, Something); printf(" %s - END_OF_LIST_BIT_MASK\n", Something); ConvertIntNodeToBinaryString(LETTER_BIT_MASK, Something); printf(" %s - LETTER_BIT_MASK\n", Something); return 0; } |
// This program tests the validity of a Blitzkrieg DAWG file, and demonstrates the new Dawg-Node configuration. // Updated on Monday, December 29, 2011. #include <stdlib.h> #include <stdio.h> #include <string.h> #define MAX 15 #define MAX_INPUT 120 #define BIG_IT_UP -32 #define LOWER_IT 32 #define SIZE_OF_CHARACTER_SET 26 #define WILD_CARD '?' #define DAWG_DATA "Traditional_Dawg_For_Word-List.dat" #define WORD_LIST_OUTPUT "New_Dawg_Word_List.txt" // These values define the format of the "Dawg" node encoding. #define CHILD_BIT_SHIFT 10 #define END_OF_WORD_BIT_MASK 0X00000200 #define END_OF_LIST_BIT_MASK 0X00000100 #define LETTER_BIT_MASK 0X000000FF // Define the boolean type as an enumeration. typedef enum {FALSE = 0, TRUE = 1} Bool; typedef Bool* BoolPtr; // When reading strings from a file, the new-line character is appended, and this macro will remove it before processing. #define CUT_OFF_NEW_LINE(string) (string[strlen(string) - 1] = '\0') // For speed, define these two simple functions as macros. They modify the "LettersToWorkWith" string in the recursive anagrammer. #define REMOVE_CHAR_FROM_STRING(thestring, theposition, shiftsize) ( memmove(thestring + theposition, thestring + theposition + 1, shiftsize) ) #define INSERT_CHAR_IN_STRING(ts, tp, thechar, shiftsize) ( (memmove(ts + tp + 1, ts + tp, shiftsize)), (ts[tp] = thechar) ) // These are the predefined characters that exist in the DAWG data file. const unsigned char CharacterSet[SIZE_OF_CHARACTER_SET] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z' }; // Enter the graph at the correct position without scrolling through a predefined list of level "0" nodes. const unsigned char EntryNodeIndex[SIZE_OF_CHARACTER_SET] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 }; // This function converts any lower case letters in the string "RawWord", into capitals, so that the whole string is made of capital letters. void MakeMeAllCapital(char *RawWord){ int X; for ( X = 0; X < strlen(RawWord); X++ ){ if ( RawWord[X] >= 'a' && RawWord[X] <= 'z' ) RawWord[X] = RawWord[X] + BIG_IT_UP; } } // This function removes any char from "ThisString" which does not exist in "CharacterSet". void RemoveIllegalChars(unsigned char *ThisString){ int X; int Y; int Length = strlen(ThisString); for ( X = 0; X < Length; X++ ) { if ( ThisString[X] == WILD_CARD ) goto CheckNextPosition; for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { if ( ThisString[X] == CharacterSet[Y] ) goto CheckNextPosition; } // The "char" in position "X" is illegal. memmove(ThisString + X, ThisString + X + 1, Length - X); X -= 1; Length -= 1; CheckNextPosition:; } } // Return the index position of character "ThisChar", as it appears in "CharacterSet", and it must exist in the set. unsigned char CharToIndexConversion(unsigned char ThisChar){ int Y; if ( ThisChar == WILD_CARD ) return 255; for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { if ( ThisChar == CharacterSet[Y] ) return Y; } } // This is a simple Bubble Sort. void Alphabetize(unsigned char *Word){ int X; int Y; int WildCardCount = 0; unsigned char WorkingChar; int WordSize = strlen(Word); for( X = 1; X < WordSize; X++ ) { for( Y = 0; Y <= (WordSize - X - 1); Y++ ) { if ( CharToIndexConversion(Word[Y]) > CharToIndexConversion(Word[Y + 1]) ) { WorkingChar = Word[Y + 1]; Word[Y + 1] = Word[Y]; Word[Y] = WorkingChar; } } } if ( Word[WordSize - 1] == WILD_CARD ) { for ( X = WordSize - 1; X >= 0; X-- ) { if ( Word[X] == WILD_CARD ) WildCardCount += 1; } memmove(Word + WildCardCount, Word, WordSize - WildCardCount); memset(Word, WILD_CARD, WildCardCount); } } // Define the "Dawg" functionality as macros for speed. "DAWG_CHILD()" Now uses only a single bit shift operation. #define DAWG_LETTER(thearray, theindex) (thearray[theindex]&LETTER_BIT_MASK) #define DAWG_END_OF_WORD(thearray, theindex) (thearray[theindex]&END_OF_WORD_BIT_MASK) #define DAWG_NEXT(thearray, theindex) ((thearray[theindex]&END_OF_LIST_BIT_MASK)? 0: theindex + 1) #define DAWG_CHILD(thearray, theindex) (thearray[theindex]>>CHILD_BIT_SHIFT) // A recursive depth first traversal of "TheDawg" lexicon to produce a readable wordlist in "TheStream". void DawgTraverseLexiconRecurse(unsigned int *TheDawg, int CurrentIndex, int FillThisPosition, char *WorkingString, int *TheCount, FILE *TheStream){ int PassOffIndex; WorkingString[FillThisPosition] = DAWG_LETTER(TheDawg, CurrentIndex); if ( DAWG_END_OF_WORD(TheDawg, CurrentIndex) ) { *TheCount += 1; WorkingString[FillThisPosition + 1] = '\0'; // Include the Windows Carriage Return char. fprintf(TheStream, "|%6d|-|%-15s|\r\n", *TheCount, WorkingString); } if ( PassOffIndex = DAWG_CHILD(TheDawg, CurrentIndex) ) DawgTraverseLexiconRecurse(TheDawg, PassOffIndex, FillThisPosition + 1, WorkingString, TheCount, TheStream); if ( PassOffIndex = DAWG_NEXT(TheDawg, CurrentIndex) ) DawgTraverseLexiconRecurse(TheDawg, PassOffIndex, FillThisPosition, WorkingString, TheCount, TheStream); } // Move through "ThisDawg" lexicon, and print the words into "ThisStream". void DawgTraverseLexicon(unsigned int *ThisDawg, FILE *ThisStream){ char *BufferWord = (char*)malloc((MAX + 1)*sizeof(char)); int *WordCounter = (int*)malloc(sizeof(int)); *WordCounter = 0; // Include the Windows Carriage Return char. fprintf(ThisStream, "This is the lexicon contained in the file |%s|.\r\n\r\n", DAWG_DATA); DawgTraverseLexiconRecurse(ThisDawg, 1, 0, BufferWord, WordCounter, ThisStream); free(BufferWord); free(WordCounter); } // This function is the core component of this program. // It requires that "UnusedChars" be in alphabetical order because the tradition Dawg is a list based structure. void DawgAnagrammerRecurse(int *DawgOfWar, int CurrentIndex, unsigned char *ToyWithMe, int FillThisPosition, unsigned char *UnusedChars, int SizeOfBank, int *ForTheCounter, Bool WildCard){ int X; char PreviousChar = '\0'; char CurrentChar; int TempIndex = DAWG_CHILD(DawgOfWar, CurrentIndex); ToyWithMe[FillThisPosition] = DAWG_LETTER(DawgOfWar, CurrentIndex) + (WildCard? LOWER_IT: 0); if ( DAWG_END_OF_WORD(DawgOfWar, CurrentIndex) ) { *ForTheCounter += 1; ToyWithMe[FillThisPosition + 1] = '\0'; printf("|%4d| - |%-15s|%s\n", *ForTheCounter, ToyWithMe, SizeOfBank? "\0": "--> TRUE ANAGRAM"); } if ( (SizeOfBank > 0) && (TempIndex != 0) ) { for ( X = 0; X < SizeOfBank; X++ ) { CurrentChar = UnusedChars[X]; if ( CurrentChar == PreviousChar ) continue; if ( CurrentChar == WILD_CARD ) { REMOVE_CHAR_FROM_STRING(UnusedChars, X, SizeOfBank - X); while ( TempIndex ) { DawgAnagrammerRecurse(DawgOfWar, TempIndex, ToyWithMe, FillThisPosition + 1, UnusedChars, SizeOfBank - 1, ForTheCounter, TRUE); TempIndex = DAWG_NEXT(DawgOfWar, TempIndex); } INSERT_CHAR_IN_STRING(UnusedChars, X, CurrentChar, SizeOfBank - X); TempIndex = DAWG_CHILD(DawgOfWar, CurrentIndex); } else { do { if ( CurrentChar == DAWG_LETTER(DawgOfWar, TempIndex) ) { REMOVE_CHAR_FROM_STRING(UnusedChars, X, SizeOfBank - X); DawgAnagrammerRecurse(DawgOfWar, TempIndex, ToyWithMe, FillThisPosition + 1, UnusedChars, SizeOfBank - 1, ForTheCounter, FALSE); INSERT_CHAR_IN_STRING(UnusedChars, X, CurrentChar, SizeOfBank - X); TempIndex = DAWG_NEXT(DawgOfWar, TempIndex); break; } else if ( CurrentChar < DAWG_LETTER(DawgOfWar, TempIndex) ) break; } while ( TempIndex = DAWG_NEXT(DawgOfWar, TempIndex) ); } if ( TempIndex == 0 ) break; PreviousChar = CurrentChar; } } } // This function uses "MasterDawg" to determine the words that can be made from the letters in "CharBank". // The words will be displayed in alphabetical order according to "CharacterSet[]". // The return value is the total number of words found. int DawgAnagrammer(int *MasterDawg, unsigned char * CharBank){ int X; int Y; int Result; int BankSize = strlen(CharBank); int *ForTheCount = (int*)malloc(sizeof(int)); unsigned char *TheWordSoFar = (char*)malloc((MAX + 1)*sizeof(char)); unsigned char *LettersToWorkWith = (unsigned char*)malloc(MAX_INPUT*sizeof(unsigned char)); unsigned char PreviousChar = '\0'; unsigned char CurrentChar; int NumberOfLetters; int CurrentEntryNode; strcpy(LettersToWorkWith, CharBank); Alphabetize(LettersToWorkWith); NumberOfLetters = strlen(LettersToWorkWith); *ForTheCount = 0; for ( X = 0; X < BankSize; X++ ) { CurrentChar = LettersToWorkWith[X]; // Move to the next letter if we have already processed the "CurrentChar". if ( CurrentChar == PreviousChar ) continue; if ( CurrentChar == WILD_CARD ) { REMOVE_CHAR_FROM_STRING(LettersToWorkWith, X, NumberOfLetters - X); for ( Y = 0; Y < SIZE_OF_CHARACTER_SET; Y++ ) { if ( EntryNodeIndex[Y] ) { DawgAnagrammerRecurse(MasterDawg, EntryNodeIndex[Y], TheWordSoFar, 0, LettersToWorkWith, NumberOfLetters - 1, ForTheCount, TRUE); } } INSERT_CHAR_IN_STRING(LettersToWorkWith, X, CurrentChar, NumberOfLetters - X); PreviousChar = CurrentChar; continue; } // Make sure not to enter the graph if NO words begin with "CurrentChar". CurrentEntryNode = EntryNodeIndex[CharToIndexConversion(CurrentChar)]; if ( !CurrentEntryNode ) { PreviousChar = CurrentChar; continue; } REMOVE_CHAR_FROM_STRING(LettersToWorkWith, X, NumberOfLetters - X); DawgAnagrammerRecurse(MasterDawg, CurrentEntryNode, TheWordSoFar, 0, LettersToWorkWith, NumberOfLetters - 1, ForTheCount, FALSE); INSERT_CHAR_IN_STRING(LettersToWorkWith, X, CurrentChar, NumberOfLetters - X); PreviousChar = CurrentChar; } Result = *ForTheCount; free(ForTheCount); free(TheWordSoFar); free(LettersToWorkWith); return Result; } int main() { int NumberOfNodes; int *TheDawgArray; FILE *Lexicon; FILE *WordList; unsigned char *DecisionInput; Bool FetchData = TRUE; unsigned char FirstChar; int InputSize; DecisionInput = (unsigned char *)malloc(MAX_INPUT*sizeof(char)); Lexicon = fopen(DAWG_DATA, "rb"); fread(&NumberOfNodes, sizeof(int), 1, Lexicon); printf("\n The lexicon DAWG contains |%d| nodes.\n", NumberOfNodes); TheDawgArray = (int *)malloc(NumberOfNodes*sizeof(int)); fread(TheDawgArray, sizeof(int), NumberOfNodes, Lexicon); fclose(Lexicon); printf("\n \"%s\" has been read into memory.\n\n", DAWG_DATA); // This program relies on a compressed lexicon data file, // so allow the user to see a readable word list in an output file. while ( FetchData == TRUE ) { printf("\nWould you like to print the Dawg word list into a text file?(Y/N): "); fgets(DecisionInput, MAX_INPUT, stdin); FirstChar = DecisionInput[0]; if ( FirstChar == 'Y' || FirstChar == 'y' ) { WordList = fopen(WORD_LIST_OUTPUT, "w"); DawgTraverseLexicon(TheDawgArray, WordList); fclose(WordList); FetchData = FALSE; } else if ( FirstChar == 'N' || FirstChar == 'n' ) FetchData = FALSE; } FetchData = TRUE; // Now the user can enter strings of letters for anagramming, to see the words that can be made from them. while ( FetchData == TRUE ) { printf("\nEnter anagram letters ( At least 2 letters) - (WildCard = ?): "); fgets(DecisionInput, MAX_INPUT, stdin); CUT_OFF_NEW_LINE(DecisionInput); MakeMeAllCapital(DecisionInput); RemoveIllegalChars(DecisionInput); InputSize = strlen(DecisionInput); if ( InputSize >= 2 ) { printf("\nThis is the set of letters that you just input |%s|.\n\n", DecisionInput); printf("\n|%d| Words were found in the lexicon Dawg.\n", DawgAnagrammer(TheDawgArray, DecisionInput)); } else FetchData = FALSE; } printf("\nThank you for testing the new Blitzkrieg DAWG encoding. GAME OVER.\n\n"); return 0; } |
